主定理计算时间复杂度

在算法导论中，主定理可以用来计算递归调用的时间复杂度，在这里给出主定理的证明和几个实例。

主定理

描述

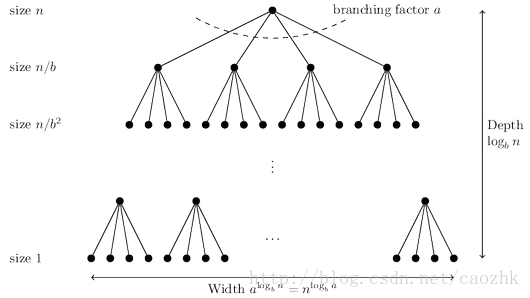
一个规模为 $n$ 的问题通过分治，得到 $a$ 个规模为 $n/b$ 的问题，每次递归带来的额外计算为 $c (n^d)$，则 $T (n)\leq aT (n/b)+c (n^d)$

问题的复杂度为

$$T (n)=\begin {equation} \left\{ \begin {array}{lr} O (n^d log (n)) & a = b^d \\ O (n^d ) & a < b^d\\ O (n^{log_b^a})) & a > b^d \end {array} \right. \end {equation}$$

证明

可见，每次递归把问题分为 a 个规模为 $n/b$ 的子问题。从根节点开始，共有 $log_b^n+1$ 层，叶子节点数为 $a^{log_b^n}$。那么，第 j 层共有 $a^j$ 个子问题，每个问题规模为 $n/b^j$，每个子问题运算量为 $c\cdot (n/b^j)^d$ 需要完成的计算量不超过：

$$a^j\cdot c\cdot (\frac {n}{b^j})^d = cn^d\cdot (\frac {a}{b^d})^j$$

整个问题的运算量

$$Tot \leq cn^d\cdot \sum_{j=0}^{log_b^n}(\frac {a}{b^d})^j$$

应用实例

二分搜索

每次规模减半，并只选择一个分支，带来的额外计算为常数级，则 $a=1,b=2,d=0$

复杂度为 $O (n^0\cdot log (n))=O (log (n))$

快排

随机选择一个锚点，划分是否平均影响复杂度

每次问题规模减半，带来额外计算次数正比于 $n$，$a=2,b=2,d=0$

复杂度为 $O (n^1\cdot log (n))=O (nlog (n))$

归并排序

数据均分为两部分，分别排序，然后以 $O (n)$ 的复杂度归并，空间复杂度为 $O (n)$

每次问题规模减半，带来额外计算次数正比于 $n$，$a=2,b=2,d=0$

复杂度为 $O (n^1\cdot log (n))=O (nlog (n))$

基数排序

最低位到最高位按位排序

每次递归问题规模变为原来的 1/10，需要求解 10 个子问题，额外运算为 $O (n)$，$a=10,b=10,d=1$

复杂度 $O (n^1\cdot log (n))=O (nlog (n))$