密码学之椭圆曲线
我们在《几何》课本里学过二元一次方程表示直线,二元二次方程表示圆锥曲线 (圆,椭圆,双曲线和抛物线),那么二元三次方程表示什么曲线呢?答案自然就是椭圆曲线。为了方便研究,大部分的二元三次方程可以简化成魏尔斯特拉斯方程的形式。其中,系数 a 和 b 需要满足条件 $4a^3 + 27b^2 \neq 0$,该条件保证方程中不会出现非奇异点以获得平滑的椭圆曲线。
椭圆曲线的形状跟椭圆毫无关系。当初数学家们在研究如何计算椭圆弧长的时候发现需要求解如下类型的积分,由于和椭圆相关,积分中的分母项 $y =\sqrt {(x^3+ax+b)}$ 便被称作椭圆曲线。
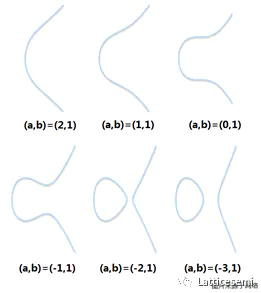
下图展示了一些合法的椭圆曲线,
下图展示了两种非法的椭圆曲线,分别存在一个尖点和叉点使曲线不平滑。
密码学与有限循环群
现代密码学算法和协议中,消息是作为有限空间中的数字或元素来处理的。加密和解密的各种操作必须在消息之间进行变换,以使变换服从有限消息空间内部的封闭性。然而,数的一般运算诸如加减乘除并不满足有限空间内部的封闭性。所以密码算法通常运行于具有某些保持封闭性的代数结构的空间中,这种代数结构就是 有限循环群 。在数学中,群是一种代数结构,由一个集合以及一个二元运算组成。群必须满足以下四个条件:封闭性,结合律,存在单位元和存在逆元。
椭圆曲线群定义
1985 年,Neal Koblitz 和 Victor S.Miller 分别独立提出利用椭圆曲线产生椭圆曲线循环群用于密码学。在数学上,椭圆曲线群的元素为椭圆曲线上的点,群操作为”+”,”+” 的定义为,给定曲线两点 $P,Q,P+Q$ 等于 $P$ 和 $Q$ 两点的连线与曲线交点沿 X 轴的对称点,如果 $P=Q$,则 $P+P$ 等于 P 在曲线上的切线与曲线交点沿 X 轴的对称点。该群的单位元为无穷远零点记作 $O=(0,0)$,有 $P+O=P$,点 P 的逆元为其沿 X 轴的对称点,记作 $-P$。
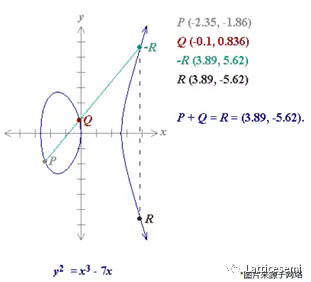
下图演示了如何计算 $P+Q=R (P\neq Q)$
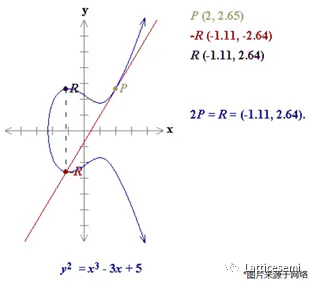
下图演示了如何计算 $P+Q=2P=R (P=Q)$。
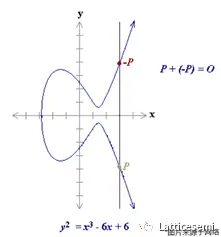
下图演示了如何计算 $P$ 的逆元 $-P$。
椭圆曲线有限循环群
前面介绍的椭圆曲线都是基于有理数的,但是计算机运算浮点数 (小数) 的速度较慢,更重要的是四舍五入浮点数会产生误差,导致多次加密解密操作后原始消息不能被还原。故考虑到加密算法的可实现性,密码学上使用基于整数的模加运算产生椭圆曲线有限循环群。
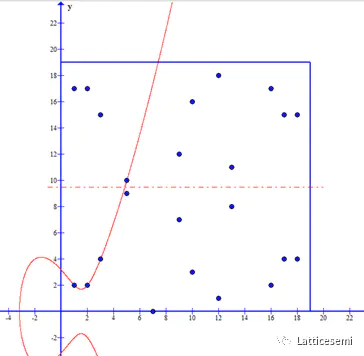
本文不涉及具体的数学计算,将用具体的例子展示如何产生 ECC 有限循环群。例如考虑 $y^2=x^3-7x+10\ (mod\ 19)$ 的集合,该集合中所有的元素如下图所示。模运算把发散的椭圆曲线映射到 $19\times 19$ 的正方形空间中,并且保持了原有曲线的上下对称特性。
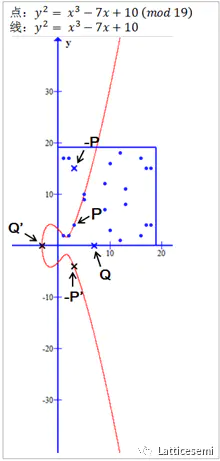
下图展示了 $y^2=x^3-7x+10\ (mod\ 19)$ 集合中的元素和椭圆曲线的关系。
点 $Q’$ 映射到点 $Q$,点 P 的对称点也由点 $-P’$ 映射到点 $-P$。
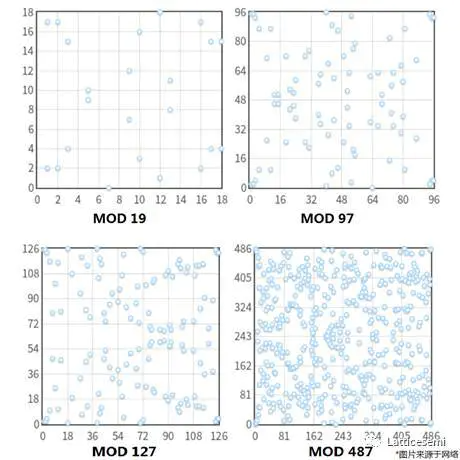
如果取一个更大的质数 $p$ 进行模运算,集合中的元素点也会相应地增多。下图展示了利用同一个曲线方程进行不同模运算的结果。在实际的椭圆曲线加密算法中,使用长度为 192-256 位的质数 $p$ 进行模运算。
现在我们基于 $y^2=x^3-7x+10\ (mod\ 19)$,利用产生元 $P=(2,2)$ 来生成 ECC 有限循环群。如下图所示。具体的计算使用 在线 ECC 计算器。
得到如下结果:
$G={nP|P=(2,2)}$ 完整的集合为
${p=(2,2),2P=(13,8),3P=(1,2), … 23P=(2,17),24P=O=(0,0)}$
椭圆曲线离散对数问题 ECDLP
请问上图中与点 $Q$ 相对应的 $n$ 值为多少?
查找集合 $G={nP|P=(2,2)}$ 中的元素可知答案是 $Q=(5,10)=10P$,但是实际应用中没有现成的集合可供查表。若已知某个点 Q,只能用比较原始的方法演算可能的 $n$ 值,目前可实现的效率最高的算法为 Baby-step giant-step 算法,计算复杂度为 $O (\sqrt {n})$。反过来,如果已知 n 计算 $n*P$ 则简单的多,因为有限循环群满足结合律,可以使用 square and multiply 算法,计算复杂度为 $O (2log2n)$。例如,比特币使用名为 secp256k1 的标准 ECC 曲线,$n$ 的长度为 256 位. Baby-step giant-step 算法的计算复杂度为 $O (2^{128})$,而 square and multiply 算法的计算复杂度仅为 O (512)。
用密码学术语描述为:ECC 有限循环群构成了一个单向函数 $Q=nP$,已知 $n,P$ 可以很容易计算 $Q$;反过来已知 $P,Q$ 则难以计算 $n$. 于是 $(n,Q=n\cdot P )$ 构成了一对私钥和公钥。
举个具体的例子,利用 square and multiply 算法计算 Q=137P,仅需 9 步便得到计算结果。
ECDH 基于椭圆曲线的 Diffie-Hellman 密钥交换
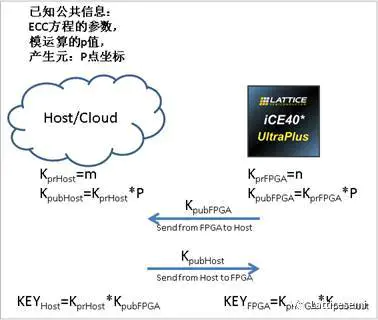
ECC 可以用于加密解密,但是由于其算法复杂计算速度慢,故莱迪思 iCE40 UltraPlus 系列芯片综合使用 ECDH 算法进行密钥交换,再通过 AES 进行消息的快速加密 / 解密助力于 IoT 通信。故本文以 iCE40 UltraPlus 芯片的 Security IP 为例介绍 ECDH 密钥交换。下图为 ECDH 密钥交换算法的示意图,iCE40Plus 和 Host 分别产生自己的私钥和公钥,然后通过公共网络把公钥分享给对方,再各自使用私钥在本地计算出相同的密钥进行 AES 加密通信。
由于有限循环群满足交换律,我们可以验证